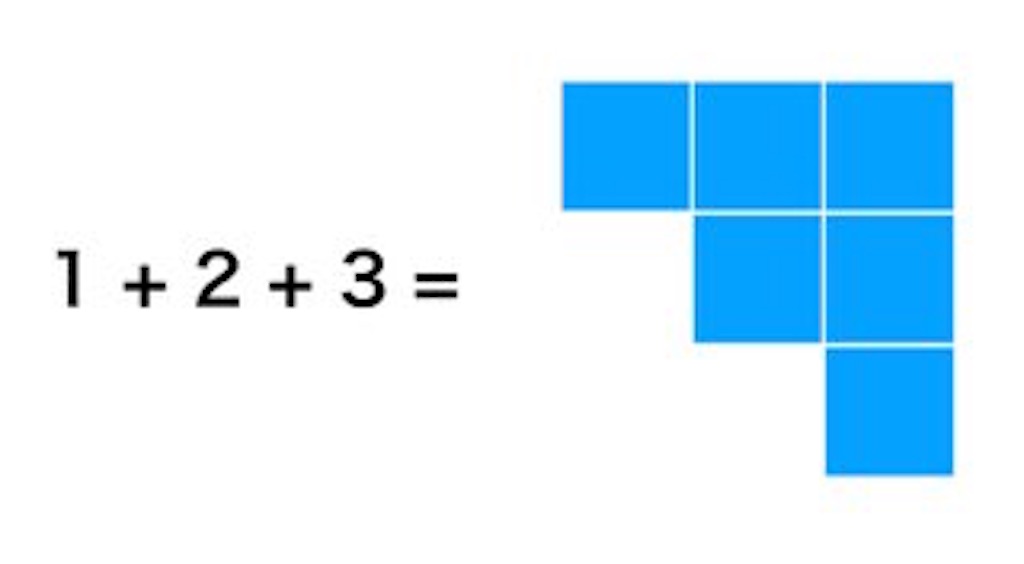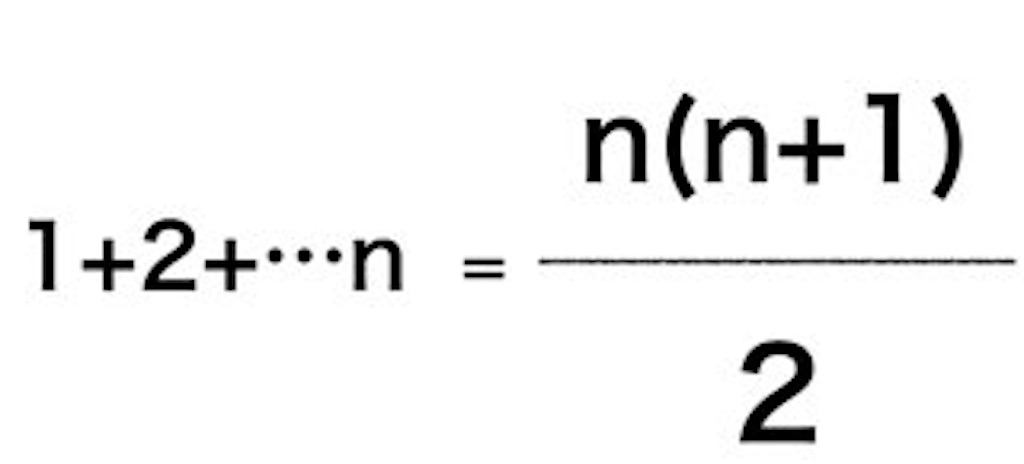こんにちは、京大生ブロガーのゲーテ(@goethe_kyodai)です。
高校数学で自然数の総和の公式ってでてきましたよね?忘れている人のために載せておくと
ですね。
高校の教科書では技巧的な方法で導出していたと思います。そこで挫折した人もいたかと思います。
そこで僕が四角形を使って数学の苦手な文系でも分かるように導出します。
まず一般のnから始めると混乱する方もいると思うのでn=3の場合から始めます。
まず、1 + 2 + 3 というのは1✖︎1の正方形ブロックを積み上げていって階段のような図形で表せます。
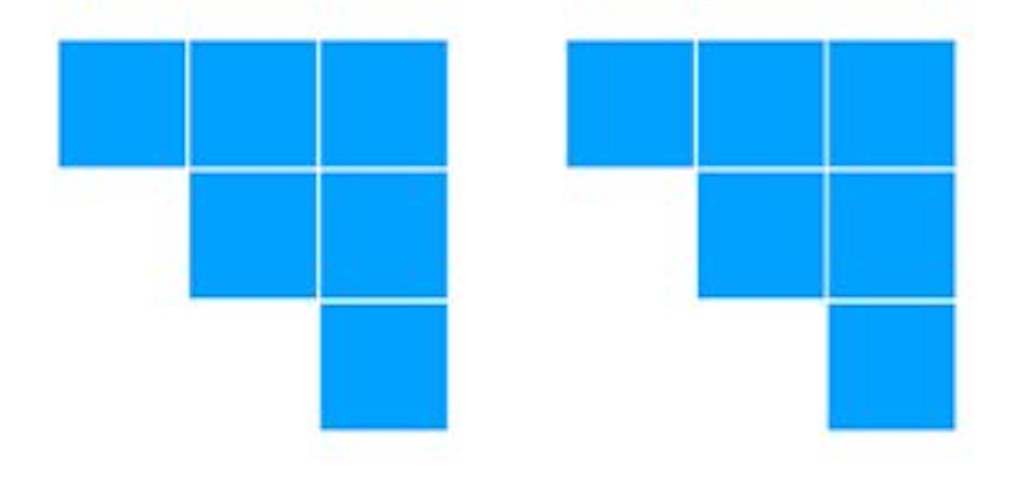
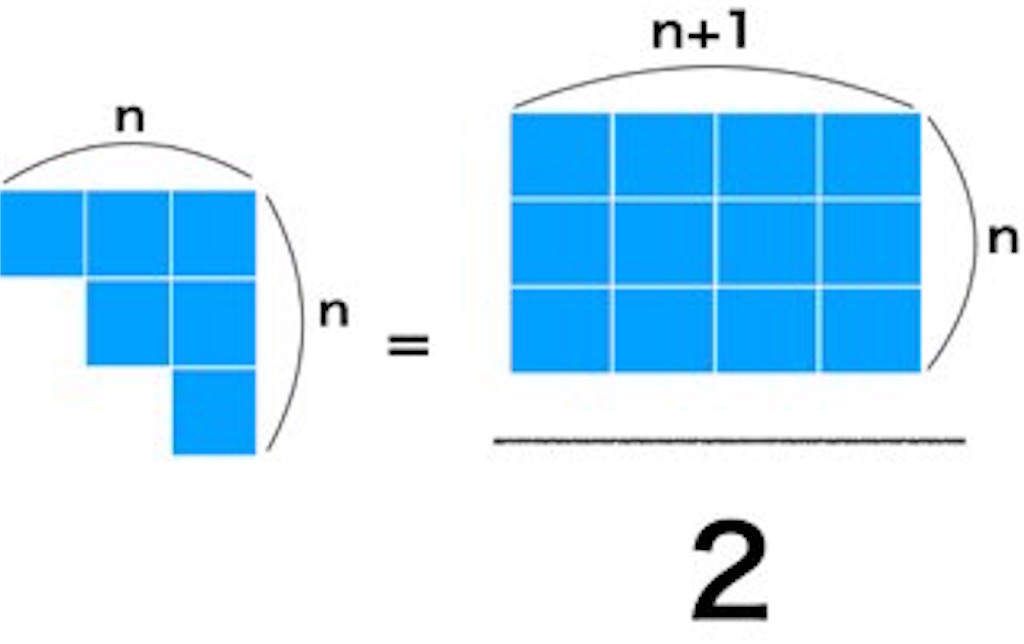
そして、その階段のような図形を二つ用意します。
いい感じにハマりそうなので合体して見ます。
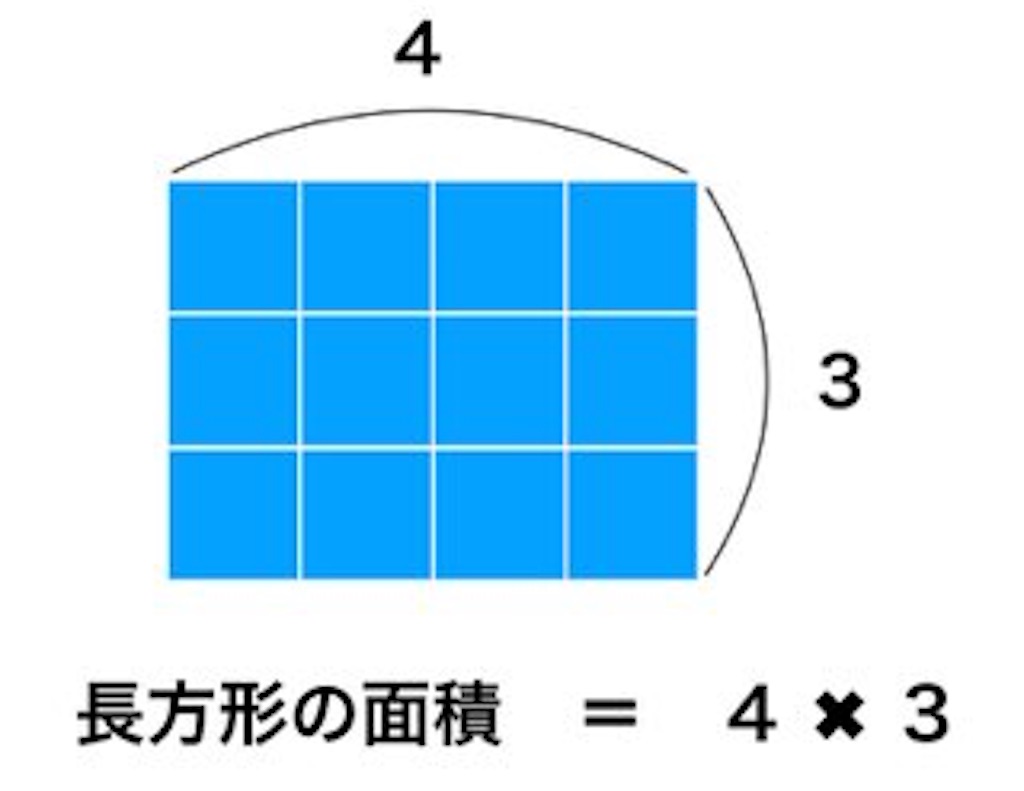
綺麗に長方形になりましたね。この長方形の面積は1+2+3が二つ集まってできたので、2(1+2+3)です。なので1+2+3は長方形の面積/2で表せます。

ところで長方形の面積はというと
縦は3、横は3に一つ足して4 なので、3 4 です。
1+2+3 = 長方形の面積/2 なので、この求めた長方形の面積3 4 を代入すればn=3の自然数の総和を求められそうですね。求めると
こうなります。
では自然数の総和の公式をnで一般化してみます。さっきの長方形の横の長さが縦の長さ+1というのがキーになってきます。
= 1 + 2 + 3 ・・・nはn=3の時みたいに階段の図形で表せて
となります。
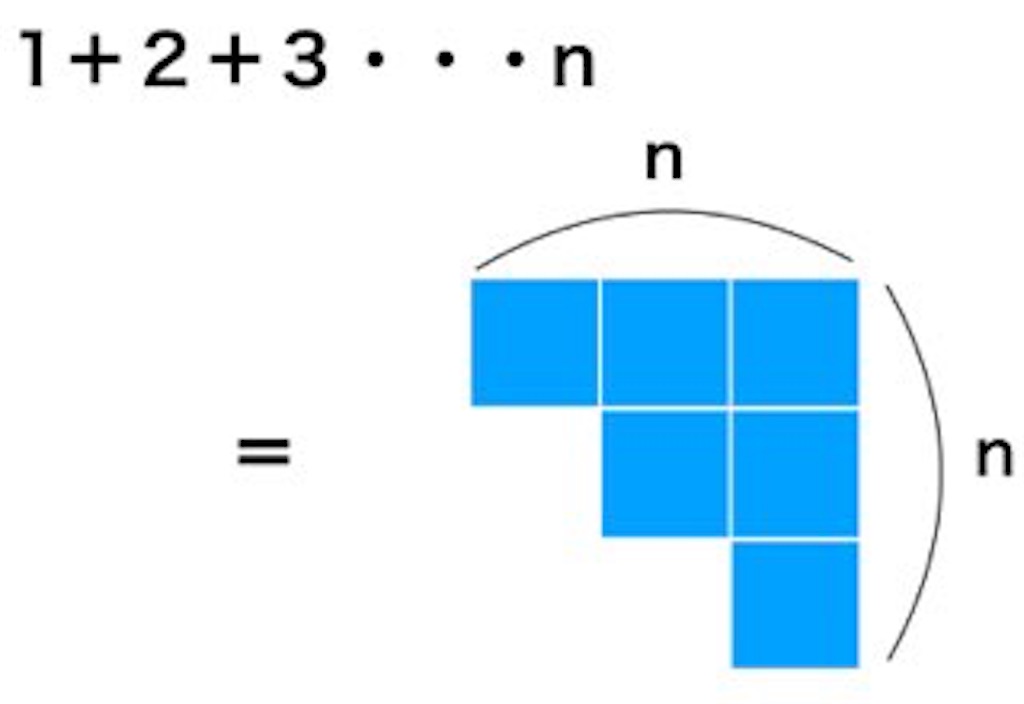
これをn=3みたいに二つ用意して合体して長方形を作ると
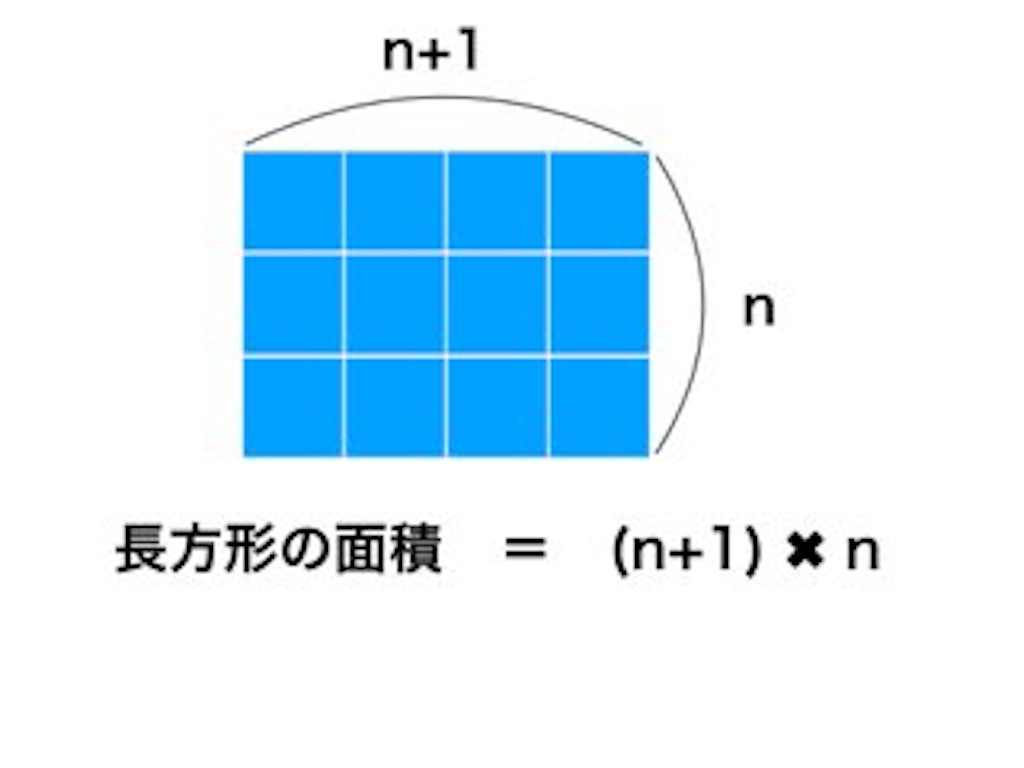
縦n、横n+1の長方形になって、面積はn(n+1)となります。
= 1 + 2 + 3 ・・・nを二つ用意して合体させた長方形の面積がn(n+1)なので、
2 = n(n+1)
ここから
と自然数の総和の公式を導き出せます!
以上のことをまとめると
こうして自然数の総和の公式が一瞬で導けます!
こういう面白い話がこの本にはたくさん載っています。数学苦手な文系でも読めるようになっているのでオススメです!