こんにちは、京大生ブロガーのゲーテ(@goethe_kyodai)です。
ことわざを理系っぽく言い換えて遊んでいたら割と面白かった ので皆さんにいくつか紹介します。早速行きましょう！
目次
犬も歩けば棒に当たる
「犬」、「歩けば」、「棒に」、「当たる」などの言葉が曖昧すぎて理系の人には耐えがたいと思うので厳密に定義して行きましょう。
犬？どの犬？ → 任意の（全ての）犬 → 記号で表すと 犬
歩けば？どこを？ → 地球上の３次元空間 → ３次元ユークリッド空間
歩けば？どうやって？ → ランダムに歩 → ランダムウォーク
棒？どの？どんな形？ → ある円柱 → 記号で表すと 円柱
当たる？何回？ → 少なくとも一回は当たる
曖昧なことわざがだいぶ厳密になりましたね。まとめてみましょう。
犬も歩けば棒に当たる
↓
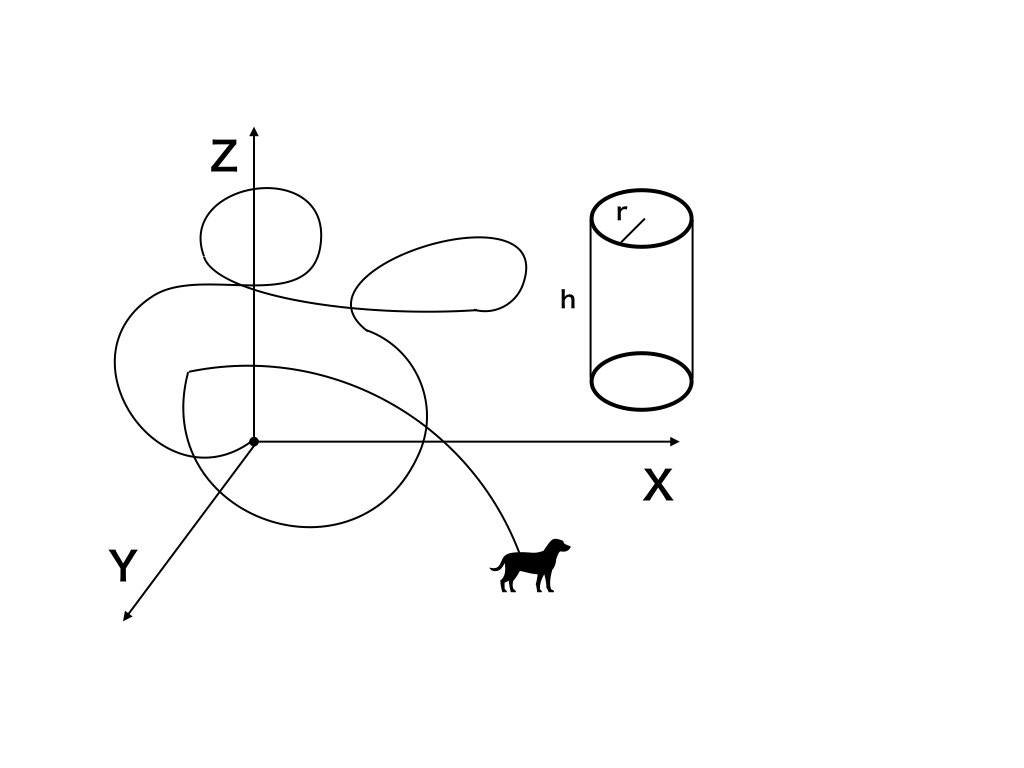
任意の犬は三次元ユークリッド空間をランダムウォークすればある円柱に少なくとも一回は当たる
※イメージ
類題：「弘法も筆の誤り」「猿も木から落ちる」を理系的に言い換えよ。（解答は読者の演習課題とする。）
不幸中の幸い
このことわざを理系的に解釈すると、「不幸」という集合の中に「幸い」と言う集合の要素が含まれると意味が取れます。
更に言い換えると、「不幸」という集合と「幸い」という集合の積集合（共通部分）が空集合では無い（存在する）となります。
数式で表すと、、、
「不幸」を集めた集合をA、「幸い」を集めた集合をBとする。A B
不幸中の幸い
↓
「不幸」という集合と「幸い」という集合の積集合は空集合ではない
※イメージ
雀の涙
これは基礎問ですね！
「雀の涙」→「ごくわずか」→ ε
εというのは理系はご存知 ε-δ論法で使わられるあのεです。言葉で言うと「0より大きい任意の実数」、数式で言うと、ε R、ε > 0です。
「0より大きい任意の実数」と言うとめちゃくちゃ大きい数を想像するかもしれませんが、「0に限りなく近いめちゃくちゃ小さい実数」と言う気持ちを表すのに使われます。
雀の涙
↓
ε
(ε
R、ε > 0)
百聞は一見に如かず
何が「如かず」なのかと言うと、「理解度」ですね。省略されてる言葉を補うと、「百聞の理解度は一見の理解度に如かず」となります。
数学的に定義してみます。f(x)をx回聞いたときの理解度を表す関数、g(y)をy回見たときの理解度を表す関数とする。「如かず」というのは不等式＞が成り立つという意味ですから、まとめると
百聞は一見に如かず
↓
f(x)をx回聞いたときの理解度を表す関数、g(y)をy回見たときの理解度を表す関数とすると、
f(100) < g(1)
恩を仇で返す
「恩を仇で返す」→「恩」を入力として「仇」を出力 → ある「恩」をパラメーターに取り、ある「仇」を返す関数
と理系ならこのことわざを当然こう言い換えますよね？
これを数式でまとめると、
恩を仇で返す
↓
f(恩) =
仇
目には目を
「目には目を」 → 目から目へ一対一対応させる → 目から目への全単射
目には目を
↓
目から目への全単射
※イメージ
山あり谷あり
山があって谷がある関数といえば？理系の皆さんなら１フェムト秒で浮かんだと思います。 はい、sin波です。
山あり谷あり
↓
sin波( 別解：cos波)
※sin波
危ない橋を渡る
橋ってこんな形してますよね？
これってあの数3で習ったあの曲線に似てません？そうです、サイクロイド曲線です。円を転がしたときにできるあの曲線です。
※サイクロイド曲線
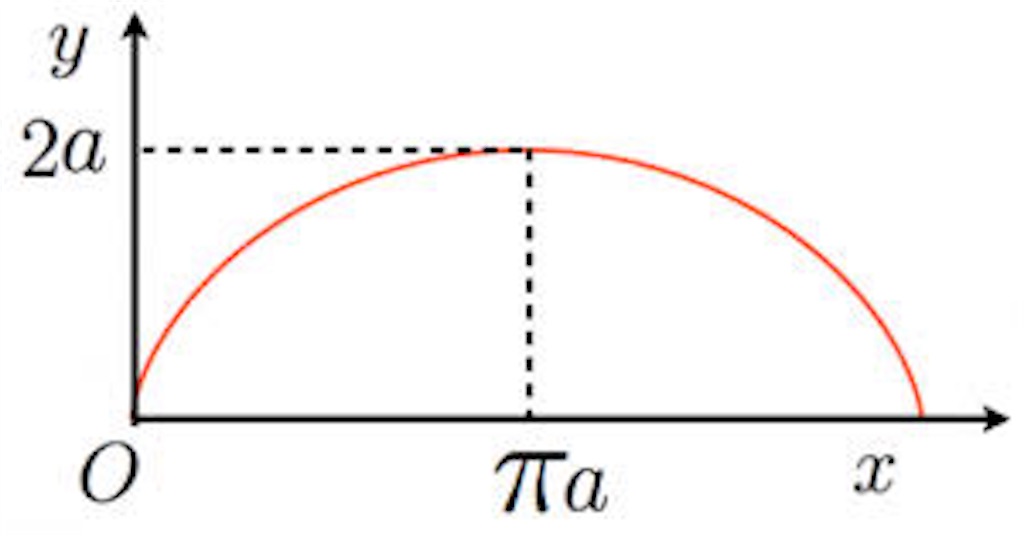
橋をサイクロイド曲線で近似してしまいましょう。
危ない橋を渡る
↓
危ないサイクロイド曲線を渡る
自業自得
「自業自得」 → 「自分でやったことは自分に返ってくる」 → 「自分のノードから自分のノードに返ってくる」
ノードというのはグラフ理論で言う「点」です。自分のノードから自分のノードに辺が返ってくるってことですね。グラフ理論ではループと言います。
自業自得
↓
ループ（グラフ理論の）
※ループ
高みの見物
理系なら「高み」と聞いたらあの言葉を連想しますよね？無限遠点です。物理では、文字通り「限りなく遠い点」ということを意味します。
高みの見物
↓
無限遠点からの見物
ことわざのまとめ
任意の犬は三次元ユークリッド空間をランダムウォークすればある円柱に少なくとも一回は当たる
「不幸」という集合と「幸い」という集合の積集合は空集合ではない
ε
f(100) < g(1)
f(恩) =
仇
目から目への全単射
sin波
危ないサイクロイド曲線を渡る
ループ
無限遠点からの見物
理系の彼氏がいる人は彼氏に使ってやるとニヤッとすること間違いなしです！
数弱なので数学的に間違ってるところがあるかもしれないのでコメントでご指摘ください！あとこんな表現の方が面白い！っていうのもジャンジャン待ってます！
